Flutterby™! : Metric System Failures 2007-10-24 13:45:57.302611+00

Metric System Failures

2007-10-24 13:45:57.302611+00 by ebradway 8 comments

A recent ruling against Seagate means that if you bought a Seagate drive in the past six or seven years, you're entitled to some money back. I was reading the postings at DailyTech where the enlightened masses were making statements like:

Sorry but just because some lazy programmers decided that 1024 was "close enough" to 1000 to call it a "kilobyte", that does not change the meaning of the SI magnitude prefixes used in just about every area of science and engineering.

Maybe the problem isn't "lazy programmers" but rather the arbitrariness of the SI system. As Dan's mentioned a few times, SI sucks for wood working. I much prefer tablespoons and cups over milliliters and grams in the kitchen. And it makes very little sense to measure something like memory, which structures in base-2 (binary), using a base-10 (decimal) system.

Where does decimal come from? Maybe it's our ten fingers (Latin digita: fingers). However, I can count to 1024 on my fingers if I use binary whereas I can only go to 10 in decimal. And an interesting bit of statistics: the average person has less than ten fingers! And no, that's not categorizing thumbs as something other than fingers. Assuming there are more people in the world who have lost a finger or two than the number of people who have extra fingers, the average comes out just less than 10! But that gets into mean vs. mode arguments...

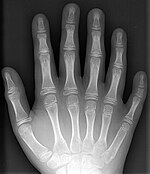These go to 11!

It always seemed to me that if you were going to efficiently use fingers for computation, a basic primitive culture would start with base 6 (possibly extending to base 36), and a sophisticated culture would use base 2. Base 10 seems like a huge lack of imagination, and totally falls apart when trying to do partial numbers.

I'd have to dig around for the proof, but I believe that it's been mathematically shown that base 60 is most universally efficient. Some think the Sumerian culture grew because their adoption of sexagesimal (base 60) numbering made conversion from other systems (used by other cultures) very easy. Base 2, Base 6, Base 10 and Base 12 all convert easily into Base 60.

Of course, just as English is becoming the standard universal language, despite it's short-comings, base 10 has long since become the universal numbering system.

It occurs to me, after dealing with several days of fucked up attempts to put GUI interfaces and such on fundamentally fairly simple underlying concepts, that the issue is simply one of audience:

Base 10 is built for the masses, the "the internet is down" and "my cupholder broke" level of person.

The further abstracted we get, the easier it may be for the drooling crowds to do something, but the harder it is to really understand what's going on under the hood and how to change the world.

But the dumbed down interface sells, and it's what gets taught to the next generation, and so we devolve.

#Comment Re: made: 2007-10-24 17:20:16.266806+00 by: ebradway [edit history]

As a Geographer, I spend a lot of time considering change in perception across scales In fact, my PhD dissertation research has to do specifically with a certain kind of representation change across scale.

As a lay-scientist in other fields, I'm acutely aware that there is really only a limited range of scales that are encompassed by Geography. The range of scale Geographers focus on is limited by human perception and experience. We generally don't talk about the geography of atoms or the geography of galaxies (but the basic concepts of spatial analysis should hold).

This is like comparing the applicable range of Newtonian Physics to Relative Physics. Newton worked well until we started getting outside our "comfort zone" of direct experience. Once we started to deal with concepts like mass greater than that of the Earth or velocities greater than sound, we needed to change the basic paradigm.

The same thing happened with units. Once we got out of our "comfort zone" that could be measured in inches and miles, we needed a paradigm that could allow us to easily compare, for instance, the mass of the Sun (1.98892 x 10^30) to the mass of a electon (9.10938188 x 10^-31). Lots and lots of orders of magnitude - 61 to be exact.

But our comfort zone only covers a few orders of magnitude. Think about the difference between the width of a hair (about 1/500 inch if you have thick hair) and the distance between Los Angeles and New York (about 12 million feet) it's only about 10 orders of magnitude. But we wouldn't ever compare those two values. If we are talking about small stuff, we might say a piece of paper is as thick (1/256 inch) as two hair-widths (if it's relatively normal 20lb stock). Or we'll compare the distance between LA and NY (2451 miles) to the distance between London and Moscow (1555 miles). Those are both within an order of magnitude - we might use two at the most. Interestingly, we'll automatically change units of measure completely when comparing across larger ranges of scale. For instance, it takes about 60 minutes for me to ride my bicycle from home to school whereas it takes me six weeks to hike the Colorado Trail from Denver to Durango. Suddenly, time is a more relevant unit of measure than actual linear distance.

I'm also more interested in how things divide into logical units. It takes about 1/2 the amount of time for me to drive to school as it does for me to bike the distance. Cutting a 1/4 of a peach pie is much more reasonable than trying to cut .2 of a peach pie.

The metric system and SI is nicely designed for comparing an extremely wide range of stuff - but human experience occurs in a much smaller range. The Imperial System developed over millennia to address our experiences in that range.

So as supporting evidence, the places I have trouble with imperial measurements are with big scaling of recipes. 8-10x of a recipe and it's teaspoons to cups to gallons. Not a huge issue, and after a few times I've no problem with it, but boundaries which I only cross occasionally.

#Comment Re: made: 2007-10-24 18:08:07.765026+00 by: ebradway [edit history]

My experience with cooking - and especially baking - is that beyond 2X or 3X, you really need to rethink the basic recipe. And I tend to drop back to ounces when I convert across more than a couple steps in units. (a tbsp = .5 oz, a cup = 8oz, a pint = 16oz, a gallon = 144oz, which, in base 8 would be tbsp = 1/2 oz, a cup = 10oz, a pint = 20oz, a gallon = 220oz).

Lately my challenge has been combining baking modifications for high elevation with changes in sweetner. Like taking a simple recipe for blueberry muffins and replacing the sugar with liquid agave syrup and making it work at 5000+ feet. I managed to get the texture right but the sweetness was way-wrong.

#Comment Re: made: 2007-10-24 20:18:35.515527+00 by: jeff [edit history]

Here is an interesting animation which attempts to add some context to orders of magnitude (in this case, powers of 10).

Eric--you're right, we typically only live in a comfort zone of a couple of orders of magnitude of scale (in typical normal daily experience, 10^-1 meters through 10^+2 meters).